Pranav Rane

Introduction

Perturbation theory is a widely used approximation method to analyze quantum mechanical systems when an analytic solution is difficult or impossible to construct. The central idea behind perturbation theory is to frame the quantum system of interest in terms of a simpler system that has been previously solved. The simpler system, which we will call the unperturbed system, is governed by the Hamiltonian \({H}^{(0)}\) which has known wavefunctions \(\psi_{n}^{(0)}(x)\) that solve the time-independent Schrodinger equation \begin{equation} {H}^{(0)} \psi_{n}^{(0)}(x) = E_{n}^{(0)} \psi_{n}^{(0)}(x) \end{equation} To frame the new quantum system in terms of the unperturbed system, we add a small perturbation term \(\delta {H}\) that, when combined with the unperturbed Hamiltonian, accurately describes the new system. Thus, in first order perturbation theory the perturbed system is now described by the Hamiltonian. \begin{equation} {H} = {H}^{(0)} + \delta {H} \end{equation} It is important that the perturbation term only has a small effect on the system for the approximation to be accurate. When solving for the total energy of the new system, we use the solutions of the unperturbed system like below \begin{equation} E_{n} = E_{n}^{(0)} + E_{n}^{(1)} = E_{n}^{(0)} + \braket{\psi_{n}^{(0)} | {H}^{(1)} | \psi_{n}^{(0)}} \end{equation} This formalization, however, breaks down when we introduce a time-dependent Hamiltonian. A common interest for chemists and physicists is to analyze the effect of electromagnetic radiation incident on an atom or molecule. The electric field of such a perturbation is inherently time dependent, so it becomes necessary to formalize how perturbation theory can generally be used in these systems. We will also see that this formalization leads us to understand phenomena such as absorption and stimulated emission, which are essential concepts to understanding laser physics. This paper concludes with a derivation of the ionization rate of hydrogen. Ionization rates of elements are important measurements that are of significance in experiments that range from chemistry, physics, and astronomy. One major application of ionization rates is in astronomy, where researchers use ionization rates of elements ranging from hydrogen to zinc to effectively characterize astrophysical spectra [4]. While calculation of these rates can be done by measurement, an understanding of the theoretical background behind ionization can lead to further insight and scientific discovery.

Time Dependence

The time dependence of quantum mechanical systems is generally introduced in introductory quantum mechanics courses. Such systems follow the time-dependent Schrodinger equation \begin{equation} \hat{H} \Psi(x,t) = i \hbar \frac{\partial \Psi}{\partial t} \end{equation} Under a time-independent Hamiltonian, the time-dependent wavefunction turns out to be the stationary state wavefunction \(\psi(x)\) multiplied by the time-dependent term \(e^{-iEt/ \hbar}\). Thus, the general time-dependent wavefunction becomes \begin{equation} \Psi(x,t) = \sum_{n} c_{n} \psi_{n}(x) e^{-iE_{n}t/ \hbar} \end{equation} However, under a time-dependent Hamiltonian this general solution for the wavefunction does not hold. The treatment of such systems will be the focus of this paper.

Single Electronic Transition of Time-Dependent Harmonic Perturbation

The system of focus will be a harmonic perturbation where the total Hamiltonian is written as \begin{equation} {H} = {H}^{(0)} + \delta {H}(t) \end{equation} where \begin{equation} \label{eq:pert_ham} \delta {H}(t) = \begin{cases} 2 H^{'} \cos{\omega t} & \text{, 0 < t < t}_{0} \\ 0 & \text{, otherwise}\\ \end{cases} \end{equation} Here, \(H^{'}\) is some time-independent term that can be used to describe a specific perturbation. The dependence on \(\cos{\omega t}\) introduces time dependence to the Hamiltonian which is only present during a defined interval of time. An arbitrary transition of the system is generally defined to go from some initial state to some final state, \(\ket{i} \rightarrow \ket{f}\). Additionally, an arbitrary state of the system can be defined as \begin{equation} \ket{\tilde{\psi}} = \sum_{n} c_{n}(t) \ket{n} \end{equation} where \(c_{n}(t)\) are time dependent coefficients that describe the amplitude to find the system in the \(\ket{n}\) eigenstate at time \(t\). Assume the coefficients have the initial conditions \begin{equation} c_{n}(0) = \delta_{ni} \end{equation} where \(i\) represents the initial state. The general formula for evaluating the transition coefficient to eigenstate \(\ket{m}\) is \begin{equation} c_{m}^{(1)} (t_{0}) = \sum_{n} \int_{0}^{t_{0}} e^{i \omega_{mn} t'} \frac{\delta H_{mn}(t')}{i \hbar} c_{n}(0) dt' \end{equation} where \(\omega_{mn}=\omega_{m}-\omega_{n}\) [\(\ref{ref:mit}\)]. Since the coefficients are initially all zero except for the initial state $i$, plugging in the initial and final states $\ket{i}$ and $\ket{f}$ leads to \begin{equation} \begin{split} c_{f}^{(1)} (t_{0}) &= \int_{0}^{t_{0}} e^{i \omega_{fi} t'} \frac{\delta H_{fi}(t')}{i \hbar} dt' \\ &= \frac{1}{i \hbar} \int_{0}^{t_{0}} e^{i \omega_{fi} t'} 2 H'_{fi} \cos{\omega t'} dt'\\ &= \frac{H'_{fi}}{i \hbar} \int_{0}^{t_{0}} \left( e^{i (\omega_{fi}+\omega) t'} + e^{i (\omega_{fi}-\omega) t'} \right) dt'\\ \end{split} \end{equation} Carrying out the integration we get \begin{equation} \label{eq:transition_amplitude} c_{f}^{(1)} (t_{0}) = -\frac{H'_{fi}}{\hbar} \left[ \frac{e^{i (\omega_{fi}+\omega) t_{0}}-1}{\omega_{fi}+\omega} + \frac{e^{i (\omega_{fi}-\omega) t_{0}}-1}{\omega_{fi}-\omega} \right]\\ \end{equation} In analyzing the two terms in Equation \(\ref{eq:transition_amplitude}\) we see that the magnitudes of the numerators of both terms are bounded to finite values because of the complex exponential. Thus, the only way for the probability amplitude of the transition \(\ket{i} \rightarrow \ket{f}\) to blow up is if either of the denominators approach zero. This leaves us with two cases to consider.

Stimulated Emission

When \(\omega_{fi}+\omega \approx 0\) the first term of Equation \(\ref{eq:transition_amplitude}\) dominates the probability of transition to state \(\ket{f}\). This means that there is a high probability of a transition when the difference in frequency between the final and initial state \(\omega_{f}-\omega_{i}\) is equal to \(-\omega\), the negative of the perturbation frequency. This corresponds to a process called stimulated emission, where there is a release of energy into the system, caused by the harmonic perturbation.

Absorption

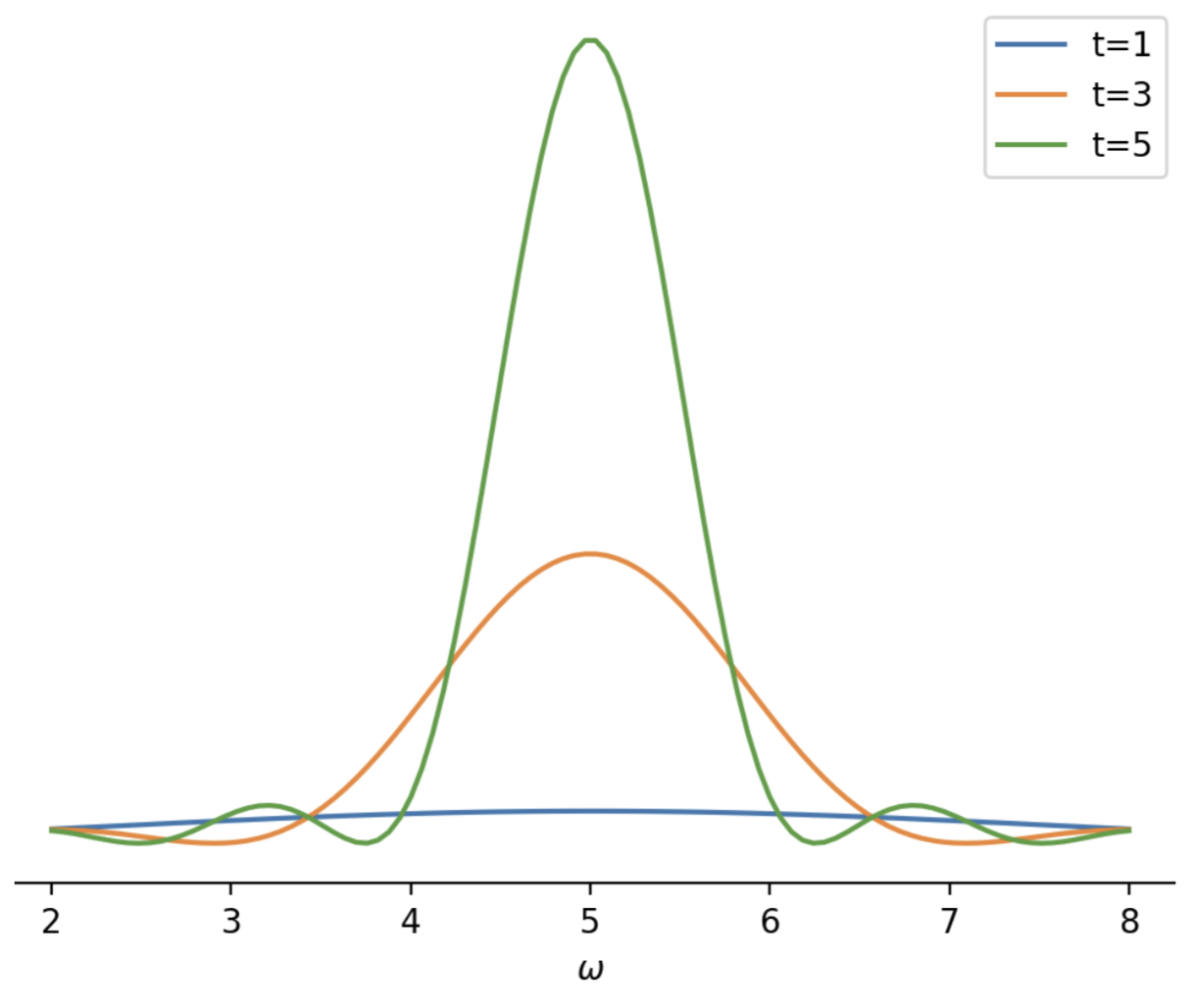
When \(\omega_{fi}-\omega \approx 0\) the second term dominates the probability of transition to state \(\ket{f}\). This process is the opposite of stimulated emission and results in the absorption of energy from the harmonic perturbation. If we analyze the transition amplitude in the case of absorption we can completely ignore the first term in Equation \(\ref{eq:transition_amplitude}\). This leaves us with a transition amplitude for the case of absorption to be \begin{equation} \label{eq:abs_trans_amp} c_{f}^{(1)} (t_{0}) = \frac{H'_{fi}}{\hbar} e^{i(\omega_{fi}-\omega)t_{0}/2} 2i \sin{(\omega_{fi}-\omega)t_{0}/2} \end{equation} where we have removed half of the phase from the complex exponential and used Euler's formula to write the \(\sin\) term. To get the probability of absorption to a final state \(\ket{f}\) we can multiply \(c_{f}^{(1)}(t_{0})\) by its complex conjugate to get \begin{equation} \label{eq:trans_prob} P_{f \leftarrow i}(t_{0}) = |c_{f}^{(1)}(t_{0})|^{2} = \frac{4 |H'_{fi}|^{2}}{\hbar^{2}} \frac{\sin^{2}[(\omega_{fi}-\omega)t_{0}/2]}{(\omega_{fi}-\omega)^{2}} \end{equation} The components that depend on \(\omega\), \(t_{0}\), and \(\omega_{fi}\) are plotted in Figure 1.

Electronic Transition to Plane Wave States

Previously we derived the probability of a single transition from state \(\ket{i}\) to \(\ket{f}\) which corresponded to absorption under harmonic perturbation. We will see shortly that when we explore the application to the ionization of hydrogen, we are interested in an electronic transition from the ground state to any final plane wave state, which describes a free electron. But how do we represent all possible plane wave states of the free electron? To explore this question, we need to introduce the concept of density of states.

Density of States

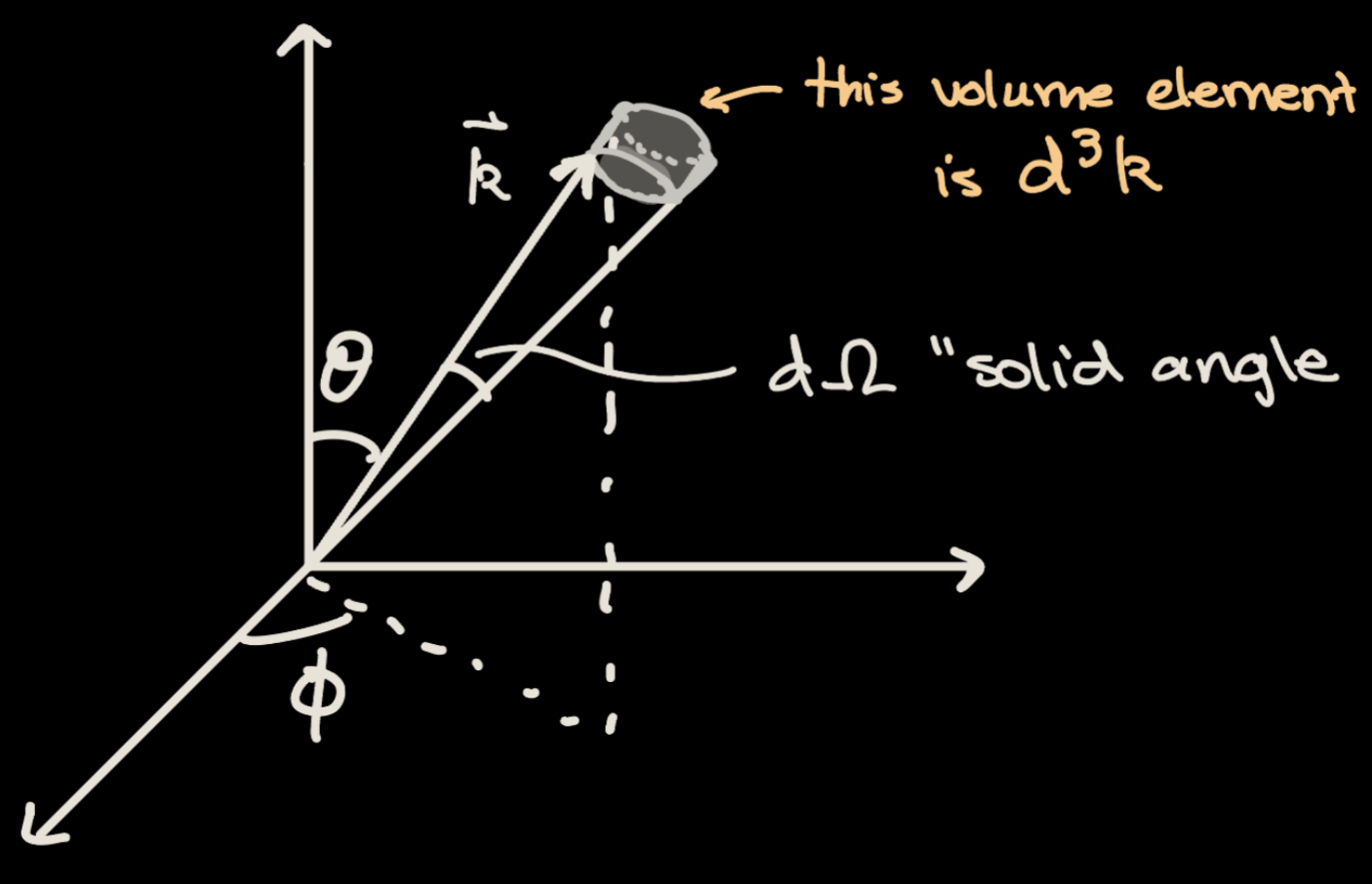
When we consider a transition to any plane wave state, we are going from a discrete space to a continuum. Imagine we put our system of interest into a large box of length \(L\). Consider a normalized wavefunction representing an arbitrary plane wave in 3-dimensions with the form \begin{equation} \psi(x,y,z) = \frac{1}{L^{3}} e^{ik_{x}x} e^{ik_{y}y} e^{ik_{z}z} \end{equation} We want this wavefunction to have periodic boundary conditions, so we impose three constraints given by \begin{equation} \begin{split} k_{x}L &= 2 \pi n_{x}\\ k_{y}L &= 2 \pi n_{y}\\ k_{z}L &= 2 \pi n_{z}\\ \end{split} \end{equation} where \(n_{x}\), \(n_{y}\), \(n_{z}\) allow for the quantization of the k values. If we let \(\vec{k}\) vary a little, we can rewrite these constraints as \begin{equation} \begin{split} dk_{x}L &= 2 \pi dn_{x}\\ dk_{y}L &= 2 \pi dn_{y}\\ dk_{z}L &= 2 \pi dn_{z}\\ \end{split} \end{equation} Thus, using these constraints, a small cube of momentum space \(d^{3}k\) can be written as \begin{equation} \begin{split} d^{3}k &= \frac{8\pi^{3}}{L^{3}} dn_{x} dn_{y} dn_{z} \\ dn &= dn_{x} dn_{y} dn_{z} = \frac{L^{3}}{8 \pi^{3}} d^{3} k \end{split} \end{equation} where \(dn\) is the number of states in an infinitesimal volume of momentum space. We will now rewrite \(d^{3}k\) by analyzing the geometry of the volume in Figure \(\ref{fig:d3k}\). This volume element is defined by the solid angle \(d\Omega\) which has the general formula \begin{equation} d\Omega = \frac{dA}{r^{2}} \end{equation} where \(dA\) is the infinitesimal area element describing the base of the volume element \(d^{3}k\) in Figure 2.

Plane Wave Transition Rate

Now that we have a form for the density of states of plane waves, we can write the probability of a transition to any plane wave as \begin{equation} \sum_{f} P_{f \leftarrow i}(t_{0}) = \int \rho(E_{f})dE_{f} P_{f \leftarrow i}(t_{0}) \end{equation} where \(P_{f \leftarrow i}\) is the probability of transition from initial state \(\ket{i}\) to some final state \(\ket{f}\) described in Equation \(\ref{eq:trans_prob}\). After substitution we get the probability of transition to any plane wave state as \begin{equation} \frac{4|H'_{fi}|^{2}}{\hbar^{2}} \rho(E_{f}=E_{i}+\hbar \omega) \int dE_{f} \frac{\sin^{2}{\frac{(\omega_{fi}-\omega)t_{0}}{2}}}{(\omega_{fi}-\omega)^{2}} \end{equation} where we have pulled out \(\rho(E)\) and \(H'_{fi}\) out from the integral since we saw in Figure 1 that majority of the integral occurs at a narrow range of energies. The other approximation we use here is that both \(\rho(E)\) and \(H'_{fi}\) are slow varying across this narrow energy range. We can evaluate this integral using the trigonometric identity \(\int \sin{x}/x^{2}=\pi\) and divide the result by \(t_{0}\) to get the transition rate \begin{equation} \label{eq:trans_rate_pw} W = \frac{2\pi}{\hbar} \rho(E_{f}=E_{i}\pm h\omega) \braket{f|H'|i}^{2} \end{equation} Here, I have included a \(\pm \hbar \omega\) term to account for the two possible transitions, stimulated emission or absorption. The quantity \(\braket{f|H'|i}\) is the expectation value of the energy of state \(\ket{f}\) after a transition from state \(\ket{i}\). This rate \(W\) describes the probability per unit time of transitioning from state \(\ket{i}\) to a plane wave state \(\ket{f}\).

Ionization of a Ground State Electron in Hydrogen

Imagine an electron in the ground state of a hydrogen atom under a harmonic electric field. What is the probability this electron will get ejected as a function of time? To answer this question using the formalization we have provided up until this point, we have to first define the problem and list our assumptions.

Assumptions

As described in Equation \(\ref{eq:pert_ham}\), the time dependent perturbation in the range \(0 < t < t_{0}\) has the form \(2H' \cos{\omega t}\). In order to simplify the problem, we want \(H'\) to have very little spatial dependence. In other words, at a particular time, the perturbed Hamiltonian that describes the system should be constant. For this to hold, we want the incoming photon to be pointed in the \(+z\)-direction and to have a large enough wavelength such that all parts of the atom "feel" the same \(\vec{E}\)-field. Thus, we want the condition \(\lambda_{photon} \gg a_{0}\) where \(a_{0}\) is the Bohr radius. Additionally, we want the ejected electron to have a high enough energy where it does not "feel" the Coulomb field of the proton, which leads to the requirement that \(E_{photon} \gg 13.6 \text{ eV}\). These conditions give the upper and lower limits of the photon frequency for which this approximation will hold. \begin{equation} 140 \text{ eV} \ll \hbar \omega \ll 2.3 \text{ keV} \end{equation} This is also equivalent to the limit \begin{equation} 3 \leq ka_{0} \leq 13 \end{equation}

Perturbed Hamiltonian

With an electric field oriented in the \(+z\)-direction, the energy of an electron at position \(\vec{r}\) will be \begin{equation} \delta \hat{H} = eE(t) \hat{z} = 2eE_{0}\cos{(\omega t)} r \cos{\gamma} \end{equation} where \(e\) is the charge of an electron, \(E_{0}\) is the amplitude of the electric field, \(r\) distance of the electron from the origin, and \(\gamma\) is the angle between \(\vec{r}\) of the electron and \(\vec{E}\). Since our formalization so far has explored the harmonic perturbation we can solve for \(H'\) as \begin{equation} \begin{split} \delta H &= 2 H' \cos{wt} = 2eE_{0} r \cos{\gamma} \cos{(\omega t)}\\ H' &= eE_{0}r \cos{\gamma} \end{split} \end{equation}

Solution to \(\braket{f|H'|i}\)

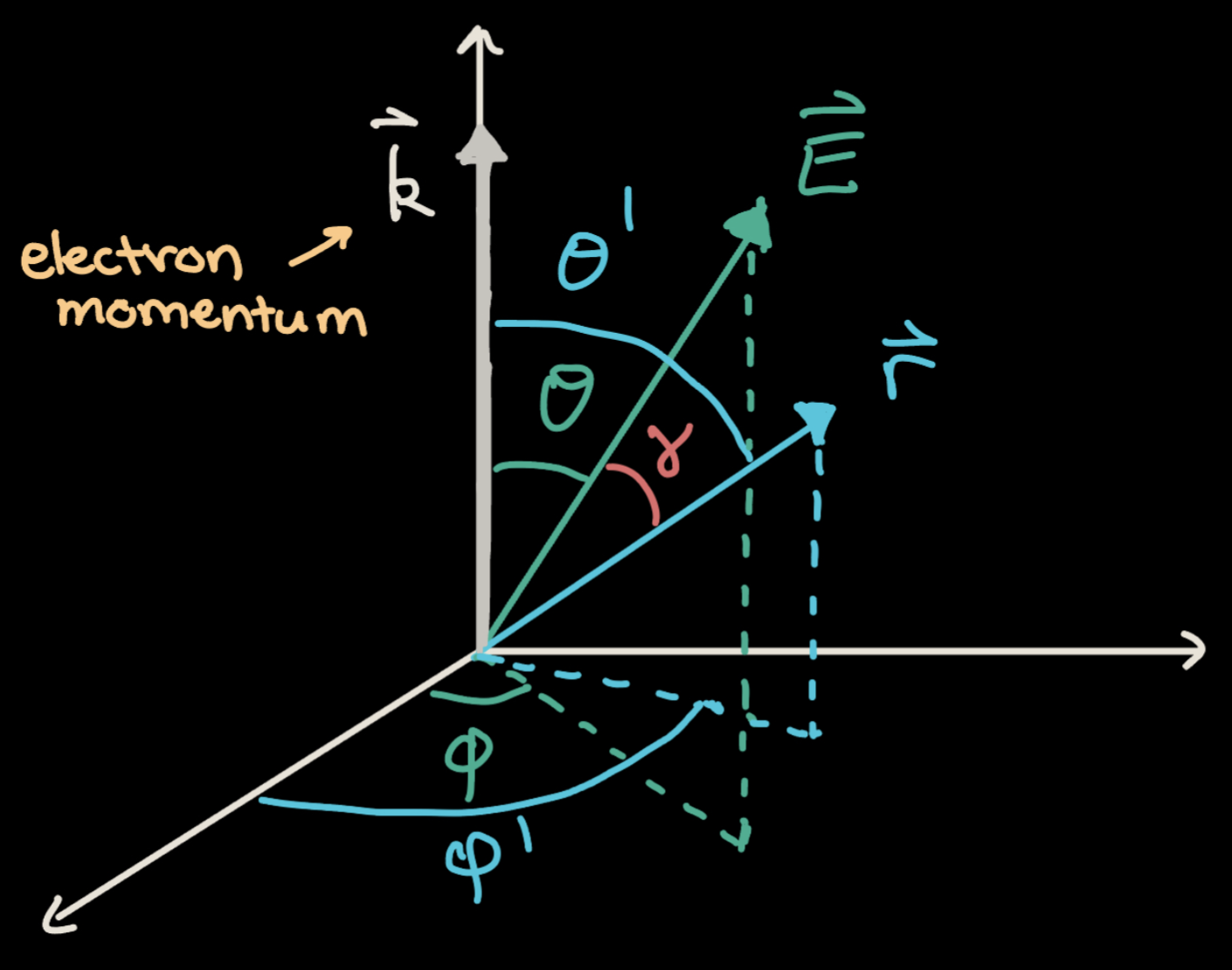
Before we continue, we will first define various angles that will be relevant to our calculation. As shown in Figure 3, \(\theta\), \(\theta'\), \(\phi\), \(\phi'\), and \(\gamma\) are all angles that describe the orientations of \(\vec{E}\), \(\vec{r}\), and \(\vec{k}\).

Ionization Rate of Hydrogen

After plugging in our result for \(\braket{f|H'|i}\) and the density of states formula into Equation \(\ref{eq:trans_rate_pw}\) we get \begin{equation} \frac{dW}{d\Omega} = \frac{256}{\pi} \frac{(eE_{0}a_{0})^{2}}{\hbar} \frac{ma_{0}^{2}}{\hbar^{2}} \frac{(ka_{0})^{3}}{(1+(ka_{0})^{2})^{6}} \cos^{2}{\theta} \end{equation} Based on the \(\cos^{2}{\theta}\) term, we can see that the electron ejection is preferable to the direction of \(\vec{E}\), which intuitively makes sense. Now integrating this across all possible values of \(\Omega\) gives our final result \begin{equation} W = \frac{512}{3} \frac{(eE_{0}a_{0})^{2}}{\hbar R_{y}} \frac{1}{(ka_{0})^{9}} \end{equation} where \(R_{y}=\frac{e^{2}}{2a_{0}}\). It is important to realize that all ejected electrons leave with momentum \(\hbar k\), which is entirely dependent on the energy of the electromagnetic radiation. We see that the ionization rate increases with the intensity of the electromagnetic radiation, \(E_{0}\), and decreases with an increase in momentum.

References

[1] Quantum Physics III — Physics. MIT OpenCourseWare. https://ocw.mit.edu/courses/8-06-quantum-physics-iii-spring-2018/.

[2] Understanding the concept of Solid Angle. https://www.youtube.com/watch?v=VmnkkWLwVsc (accessed 2024- 05-09).

[3] Mcquarrie, D. A. Quantum Chemistry; University Science Books: Sausalito, 2008.

[4] Dere, K. P. Ionization Rate Coefficients for the Elements Hydrogen through Zinc. Astronomy and Astrophysics 2007, 466 (2), 771–792. https://doi.org/10.1051/0004-6361:20066728.