Experiments with Photons

Abstract

Quantum mechanics has proved to be an extremely successful theory and has been verified by experiments over the past century. Its description and predictive power not only demystifies properties of microscopic systems but also guides philosophical questions about realism and locality. This study confirms the existence of photons through spontaneous parametric down conversion of photons with a measured degree of second order coherence, $g_{2}(0)=0$, indicating a single-photon source. This study also confirms the contradiction of local realistic theory at the microscopic scale. The Clauser-Horne-Shimony-Holt (CHSH) inequality defines the parameter $S$, where local realistic theory requires $S \leq 2$. Sixteen measurements of coincidence counts of photon pairs at various polarization angles leads to $S=2.3 \pm0.03$, indicating that photons do not abide by classical notions of reality and localism.

Introduction

Before the 1900s, the theory of light as a continuous wave was accepted and confirmed by a multitude of theories including diffraction, refraction, reflection, and dispersion. The notion of the existence of photons began with Einstein's 1905 paper introducing the conception of light as individual packets of energy. After Robert Milliken's experiment in 1915, the existence of photons was widely accepted. However, in the 1950s, the Hanbury Brown and Twiss (HBT) experiment used an attenuated light source to show that photons were detected simultaneously after a beam splitter, contradicting the particle nature of light. Later on it was shown that attenuated light sources as used in the original HBT experiment are not an ideal single photon source. Developments in laser physics in the late 1970s led to single photon sources with anti-bunching properties, which allowed the HBT experiment to confirm the particle nature of light.

Spontaneous parametric down-conversion

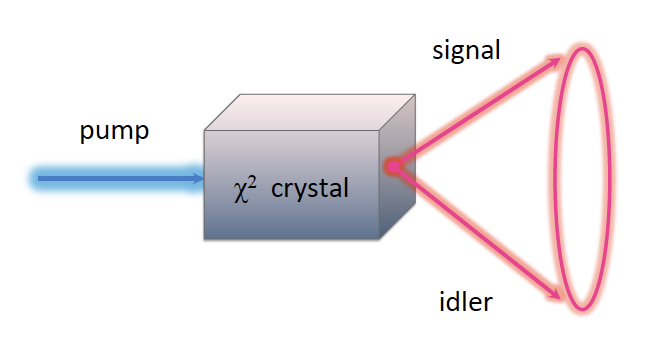
In this study, we will perform the HBT experiment using spontaneous parametric down-conversion (SPDC) of a pump laser as the single photon source. SPDC is a process in which light of a particular frequency is converted into light of a different frequency. In this experiment, Type I SPDC is used to take a photon and emit a pair of photons correlated in energy and polarization via a beta-Barium Borate (BBO) crystal (Fig. 1). Photon pairs are polarized parallel to each other and perpendicular to the pump photon. Furthermore, these pairs are emitted at the same time to a very high precision.

Figure 1. Pump photons enter BBO crystal and form photon pairs known as signal and idler photons. SPDC is a weak process, occuring about once in $10^{8}-10^{9}$ photons. Photon pairs are correlated in energy and polarization.

An important property of SPDC via a BBO crystal is that pump light polarized parallel or perpendicular to the crystal axis experience different indices of refraction $n_{e}$ and $n_{o}$, respectively, given by \begin{equation} n_{e}(\lambda) = \left (2.3753+\frac{0.01224}{(\lambda /1 \mu m)^{2}-0.01667}-0.01516(\lambda /1 \mu m)^{2} \right )^{1/2} \end{equation} \begin{equation} n_{o}(\lambda) = \left (2.7359+\frac{0.01878}{(\lambda /1 \mu m)^{2}-0.01822}-0.01354(\lambda /1 \mu m)^{2} \right )^{1/2} \label{eq:ordinary} \end{equation} These two mediums are placed one after the other in the BBO crystal and are where SPDC occurs depending on the polarization of the incoming photon. Thus, a vertically polarized photon of wavelength $\lambda_{pump}$ incident on the BBO crystal will pass through the first medium with index of refraction $n_{e}(\lambda_{pump})$ and then produce a photon pair in the next medium. On the other hand, a horizontally polarized photon of wavelength $\lambda_{pump}$ will create a pair in the first medium and travel through the second medium at an index of refraction of $n_{o}(\lambda_{pair})$. Due to photons with different polarizations passing through the BBO crystals with different indices of refraction, there is a slight time shift between the two polarizations which weakens the purity of entanglement of the photon pairs. To account for this a correctly-oriented quartz crystal can be used to pre-delay the time of photons in one polarization relative to the other prior to entering the BBO crystal.

Degree of second-order coherence

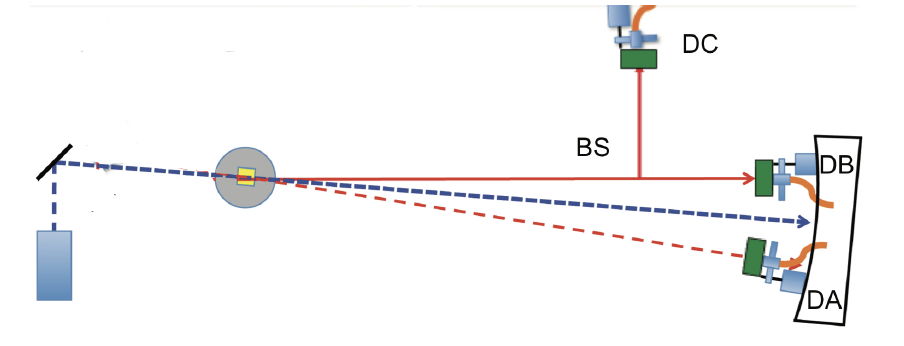
A single photon incident on a beam splitter has the ability to prove that photons exist. If light has a particle nature, then a photon will undergo either transmission or reflection after the beam splitter. If light is a classical wave then part of the wave would transmit and the other part would reflect. Thus, with detectors B and C at the two outputs of the beam splitter, the degree of second-order coherence can be written as \begin{equation} g_{2}(0) = \frac{P_{BC}}{P_{B}P_{C}} \label{eq:g2} \end{equation} where $P_{B}$, $P_{C}$, and $P_{BC}$ indicate the probability of detection at detectors $B$, $C$, and both simultaneously, respectively. This anticorrelation parameter equals zero when the incident light is a single photon source and will be non zero otherwise.

Entanglement of photon pairs

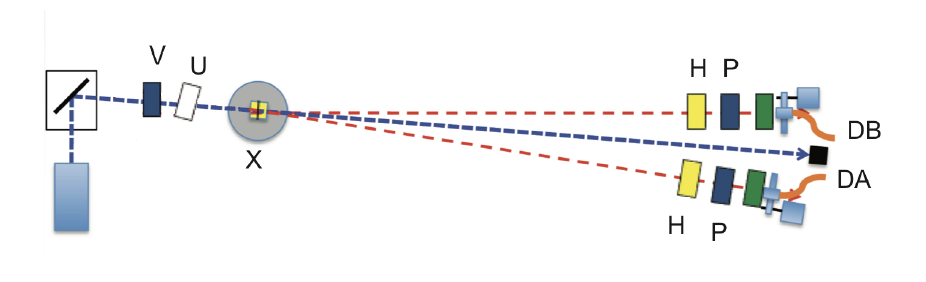
As discussed previously, SPDC can be harnessed to create photon pairs. With the use of a quartz crystal to pre-delay a certain polarization, photons polarized at 45 degrees incident on the BBO crystal can create the entangled state \begin{equation} \ket{\psi}=\frac{1}{\sqrt{2}} \left(\ket{H}_{1} \ket{H}_{2} + \ket{V}_{1} \ket{V}_{2} \right) \label{eq:entangledState} \end{equation} Entangled states are in a superposition, meaning upon creation we do not know if the photons are both horizontally or vertically polarized until measurement. Photon pairs in this state have a 50 percent chance to be measured in the horizontal basis and a 50 percent chance to be measured in the vertical basis. However, photon pairs in a mixed state of 50 percent horizontal and 50 percent vertical also have the same probabilities. \[ \ket{\psi} = \begin{cases} \ket{H_{1}}\ket{H_{2}} & p=0.5 \\ \ket{V_{1}}\ket{V_{2}} & p=0.5 \end{cases} \] It turns out that when measuring in bases at different angles the probabilities of joint detection are different for entangled and mixed states. Specifically, when measuring in the diagonal and anti-diagonal states \begin{equation} \ket{D}=\frac{1}{\sqrt{2}} \left(\ket{H} + \ket{V} \right) \label{eq:diagonal} \end{equation} \begin{equation} \ket{A}=\frac{1}{\sqrt{2}} \left(-\ket{H} + \ket{V} \right) \label{eq:antidiagonal} \end{equation} the joint probabilities for the entangled state become \begin{equation} P_{DD} = 1/2 \end{equation} \begin{equation} P_{AA} = 1/2 \end{equation} \begin{equation} P_{DA} = 0 \end{equation} \begin{equation} P_{AD} = 0 \end{equation} Whereas the joint probabilities for the mixed state become \begin{equation} P_{DD} = 1/4 \end{equation} \begin{equation} P_{AA} = 1/4 \end{equation} \begin{equation} P_{DA} = 1/4 \end{equation} \begin{equation} P_{AD} = 1/4 \end{equation} This difference in probabilities is what will be used in a Bell test of local realism, which will distinguish between the entangled state and the mixed state.

Clauser-Horne-Shimony-Holt inequality

The Clauser-Horne-Shimony-Holt (CHSH) inequality is a version of the Bell inequality that will be used in this experiment. CHSH defines a variable $E$ which describes the correlation between the polarizations of two photons. If the photons are perfectly correlated then $E=1$. If the photons are perfectly anticorrelated with state $\ket{\psi}=\frac{1}{\sqrt{2}} \left(\ket{H}_{1} \ket{V}_{2} - \ket{V}_{1} \ket{H}_{2} \right)$, then $E=-1$. If the photons are uncorrelated, then $E=0$. The variable $E$ is defined for arbitrary angles $\theta_{1}$ and $\theta_{2}$ that the polarization axis of each photon makes with the horizontal. In terms of coincidence counts $E$ can be written as \begin{equation} E(\theta_{1},\theta_{2}) = \frac{N(\theta_{1},\theta_{2})+N(\theta_{1}+\frac{\pi}{2},\theta_{2}+\frac{\pi}{2})-N(\theta_{1},\theta_{2}+\frac{\pi}{2})-N(\theta_{1}+\frac{\pi}{2},\theta_{2})}{N(\theta_{1},\theta_{2})+N(\theta_{1}+\frac{\pi}{2},\theta_{2}+\frac{\pi}{2})+N(\theta_{1},\theta_{2}+\frac{\pi}{2})+N(\theta_{1}+\frac{\pi}{2},\theta_{2})} \label{eq:e} \end{equation} where $N(\theta_{1},\theta_{2})$ is the number of coincidence counts when the first photon is measured at polarization $\theta_{1}$ and the second photon is measured at $\theta_{2}$. When measuring the entangled state in Eq. \ref{eq:entangledState} using $\theta_{1}=\theta_{2}$, Eq. \ref{eq:e} always equals 1. However, it can be shown that for mixed states $E$ follows \begin{equation} E_{mixed} = cos(2\theta_{1})cos(2\theta_{2}) \end{equation} Thus, there exists certain angles $\theta_{1}$ and $\theta_{2}$ where entangled and mixed states give different values for $E$. CHSH defines a variable $S$ that depends on four angles \begin{equation} S = E(\theta_{1},\theta_{2})-E(\theta_{1},\theta_{2}^{'})+E(\theta_{1}^{'},\theta_{2})+E(\theta_{1}^{'},\theta_{2}^{'}) \label{eq:Seq} \end{equation} Quantum mechanics predicts that entangled particles are non-local. Non-locality implies that two particles can ``know'' the state of one another instantaneously upon measurement, even at great distances. Entangled particles are also predicted to be non-real, meaning the state of either particle is undefined until it is measured. Many classical theories require locality and realism, which is what we experience in the macroscopic world. It has been shown that a local realistic theory must satisfy \begin{equation} S \leq 2 \end{equation} A maximum violation of this inequality occurs when the angles for Eq. \ref{eq:Seq} are $\theta_{1}=0$, $\theta_{2}=22.5$, $\theta_{1}^{'}=45$, and $\theta_{2}^{'}=67.5$.

Experimental Methods

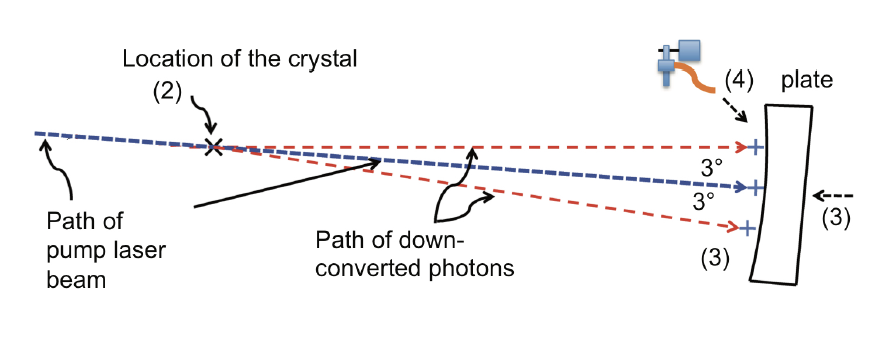
The arrangement for setting up SPDC is shown in Fig. 2. A 405nm wavelength, horizontally polarized GaN diode laser is used as the pump laser in the setup. Two photon detectors with FGL780 long pass filters are placed on the curved plate in the path of down-converted photons. One detector is carefully positioned along the curved plate to maximize the number of photon counts due to SPDC. Then, the second detector is positioned along the plate to maximize the number of coincidence counts measured between the two detectors. For the entirety of the study, a coincidence window of 7.39 ns is used. Total raw counts and coincidence counts are collected for various dwell times.

Figure 2. Experimental setup to detect photon pairs.

The HBT experiment to confirm the existence of photons is setup as in Fig. 3. A beam splitter is placed in the path of one of the down-converted photons. Additionally, a third detector is placed into the path of reflection from the beam splitter. Coincidence counts are collected between each pair of detectors and between all three detectors.

Figure 3. HBT experimental setup.

To test the locality and realism of photons, entangled photons are created as described by Eq. \ref{eq:entangledState}. The arrangement to create entangled states and measure at various polarization angles is given in Fig. 4. A 405 nm, zero order half-wave plate (V) is placed in front of the BBO crystal (X). A quartz compensating crystal (U) is placed in between (V) and (X). Both detectors have a horizontal polarizer (P) and an 810 nm, zero order half-wave plate (H) in front of them. First, the half-wave plates (H) are set to 45 degrees and the half-wave plate (V) is set to 0 degrees. This is so vertically polarized down-converted photons can be detected. The BBO crystal (X) is then tilted about the vertical axis to maximize coincidences. Now, (V) is set to 45 degrees and both (H) are set to 0 degrees to detect horizontally polarized down-converted photons. The crystal (X) is then tilted about the horizontal axis to maximize coincidence counts. As discussed previously, a quartz crystal (U) can be used to correct the temporal distinguishability that arises from the BBO crystal. To align (U), the pump photons are set to be polarized at 45 degrees by setting (V) to get equal coincidence counts when detecting vertically and horizontally polarized down-converted photons. The half-wave plates (H) are set to detect one photon in the state described by Eq. \ref{eq:diagonal} and the other photon in state described by Eq. \ref{eq:antidiagonal}. This is done by setting one half-wave plate (H) to 22.5 degrees and the other to -22.5 degrees. The quartz crystal (U) is then tilted about the vertical axis until coincidences are a minimum. Eq. \ref{eq:Seq} leads to coincidence measurements at sixteen different angles. The half-wave plates (H) are varied to detect the desired angles as shown in Eq. \ref{eq:e}. In order to set the correct angles on (H), the angle is set to the sum of the desired measurement angle divided by two and the fast axis angle. Each measurement is run for a dwell time such that there is a minimum of 400 coincidence counts. The number of coincidences and the dwell time for each measurement is collected.

Figure 4. Experimental setup to test CHSH inequality.

Results and interpretation

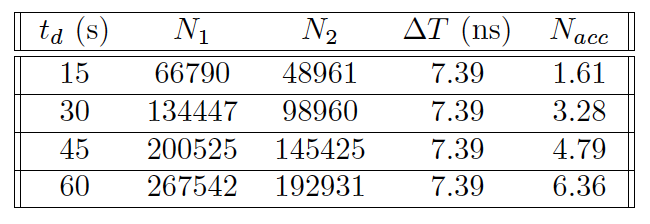
Due to environmental factors in the laboratory, there is some probability some of the coincidence counts to be accidental detections. The number of accidental coincidences can be calculated via probabilistic arguments and is given by \begin{equation} N_{acc} = \frac{N_{1}N_{2} \Delta T}{t_{d}}, \label{eq:bandwidth} \end{equation} where $N_{1}$ and $N_{2}$ are the raw counts for each detector, $\Delta T$ is the coincidence window in seconds, and $t_{d}$ is the dwell time. Given a range of dwell times, the results for accidental counts are given in Table 1. As described by the equation, the number of accidental counts is proportional to the dwell time.

Table 1. Raw counts for accidental coincidence calculation.

A dwell time of 60 seconds was used for the HBT experiment. The raw counts for each detector were $N_{A}=729829$, $N_{B}=277393$, and $N_{C}=339070$. The number of coincidences between both pairs of detectors were $N_{AB}=483$ and $N_{AC}=691$, and the number of triple coincidences was $N_{ABC}=0$. Rewriting Eq. \ref{eq:g2} to be compatible with SPDC gives the degree of second-order coherence as \begin{equation} g_{2}(0) = \frac{N_{ABC}N_{A}}{N_{AB}N_{AC}} \label{eq:g2new} \end{equation} Since there were no triple coincidences, $g_{2}(0)=0$, which suggests SPDC is an ideal single photon source. Completion of the sixteen measurements gave the coincidence counts and dwell times in Table 2 and Table 3, respectively.

Table 2. Coincidence counts for measurements at sixteen different polarization angles.

Table 3. Dwell times for the sixteen measurements in seconds.

Each measurement from Table 2 can be divided by the corresponding dwell times in Table 3 to get a count rate for each measurement. Then, count rates can be plugged into Eq. \ref{eq:e} to solve for the parameter $E$ for the angles of interest. This gives the values \begin{equation} E(0,22.5) = 0.172 \end{equation} \begin{equation} E(0,67.5) = -0.876 \end{equation} \begin{equation} E(45,22.5) = 0.783 \end{equation} \begin{equation} E(45,67.5) = 0.468 \end{equation} Finally, plugging these values of $E$ into Eq. \ref{eq:Seq} the parameter $S$ is calculated to be \begin{equation} S = 2.30 \pm 0.03 \end{equation} An error of 0.03 was calculated via propagation of errors, where the uncertainties in coincidence counts are due to statistical errors: $\Delta N = \sqrt{N}$. Therefore, the down-converted photons are in fact entangled and break classical notions of locality and realism.

Discussion

While the HBT experiment resulted in a degree of second-order coherence $g_{2}(0)=0$ signifying an ideal single-photon source, it is important to note that a dwell time of 60 seconds is not long enough to put an error on the calculation. Through propagation of errors and the statistical errors in counts $\Delta N = \sqrt{N}$, the error for $g_{2}(0)$ can be written as \begin{equation} \Delta g_{2}(0)=g_{2}(0) \left( \frac{1}{N_{ABC}}+\frac{1}{N_{AB}}+\frac{1}{N_{AC}}+\frac{1}{N_{A}} \right)^{1/2} \end{equation} However, with $N_{ABC}=0$, the first term in undefined. Thus, to get an error on $g_{2}(0)$, a value of $N_{ABC} \geq 1$ is needed which would require a longer dwell time.

References

[1] Walter F. Smith (2020) Experimental Physics: Principles and Practice for the Laboratory, Taylor and Francis Group.

[2] David D. Nolte (2021) A Short History of the Photon, Galileo Unbound, https://galileo-unbound.blog/2021/01/18/a-short-history-of-the- photon/ ftn1

Pranav Rane

Experiments with Entangled Photons